



Next: Aligning the collimator
Up: The collimator
Previous: The collimator
Contents
Preparing the angles of the
collimator
The collimator mirrors are 20 cm long, have a width of 3.8 cm, and are
separated 6 cm from each other. Each mirror is placed in the frame of the
collimator leaning on 4 points (see figure 2.2). The
mirror is pushed against these four supporting points with a screw. The
frame of the collimator is designed in such way that each pair of mirrors
will be almost perfectly parallel to each other.
Figure 2.2:
Attachment of the mirror on the frame of the collimator
 |
To obtain an angle between the two mirrors we have put pieces of silver
foil between the supporting point and the coated side of the mirror.
The position of the mirrors of the collimator is very critical. The angle
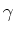 between the two mirrors is approximately 1.4 mrad, which means
that the distance between the two mirrors should change 140
between the two mirrors is approximately 1.4 mrad, which means
that the distance between the two mirrors should change 140 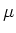 m over a
distance of 10.6 cm. This corresponds to about 10 to 14 foils. Since
the foils are not all the same thickness, it is not easy to adjust the
angles. Not only should the angle
m over a
distance of 10.6 cm. This corresponds to about 10 to 14 foils. Since
the foils are not all the same thickness, it is not easy to adjust the
angles. Not only should the angle 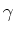 , needed for the curving of the
wavefront be correct, but it is also important not to create an angle
, needed for the curving of the
wavefront be correct, but it is also important not to create an angle
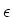 , perpendicular to the angle
, perpendicular to the angle 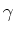 .
.
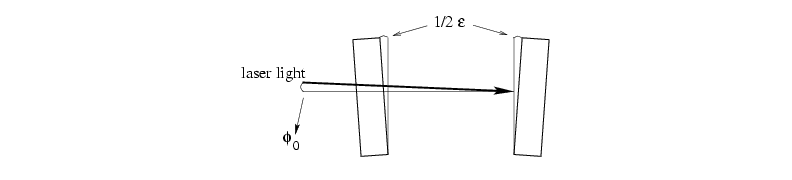
Figure 2.3:
The angles 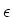 and
and 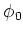 , front view of the
collimator
, front view of the
collimator
 |
This angle is created when the foils in the upper supporting point are not
of the same thickness as the foils on the lower supporting point. The
angle 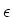 causes the laser light shining in the collimator to slowly
drift upwards or downwards away from the middle of the mirrors. Since the
atoms of the source are going through the middle of the collimator, the
angle
causes the laser light shining in the collimator to slowly
drift upwards or downwards away from the middle of the mirrors. Since the
atoms of the source are going through the middle of the collimator, the
angle 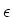 will cause a smaller overlap between the light and the
atoms, making the collimator less efficient. The angle
will cause a smaller overlap between the light and the
atoms, making the collimator less efficient. The angle 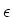 can be
changed by placing special silver foils of 2
can be
changed by placing special silver foils of 2 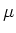 m between the
upper/lower two supporting points and the mirror when
the light was moving respectively downwards/upwards.
m between the
upper/lower two supporting points and the mirror when
the light was moving respectively downwards/upwards.
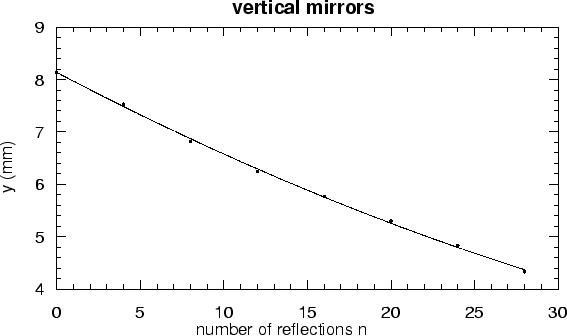
Since the angles 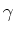 and
and 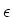 are so small, we need a special way to
measure them. In Eq. 1.11,
are so small, we need a special way to
measure them. In Eq. 1.11, 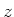 is given as a function
of the number of reflections
is given as a function
of the number of reflections 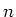 . This can be rewritten to:
. This can be rewritten to:
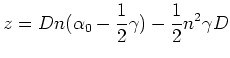 |
|
|
(2.3) |
Now we shine through the two horizontal mirrors of the
collimator with a diode laser, and we make sure the light comes out at the
other side of the
collimator. A diaphragm is inserted directly behind the diode laser to
define a smaller spot of light. We now place a diode in the collimator,
which can be translated in the z direction over the centerline of the
collimator. This diode is sensitive for the laser light used, and can
only detect even reflections, since the diode is turned towards one of the
mirrors. The diode is placed on an optical rail, and the position of the
maximum of the laser light at different reflections can be determined
accurately to a few tenths of a millimeter. We now measure the
exact position 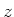 of the maximum intensity of the laser beam at different
values of
of the maximum intensity of the laser beam at different
values of 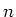 (see fig. 2.4). If we make a quadratic fit (
(see fig. 2.4). If we make a quadratic fit (
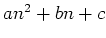 ) to these data, the angle
) to these data, the angle 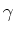 can be evaluated from
the quadratic part:
can be evaluated from
the quadratic part:
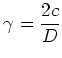 |
|
|
(2.4) |
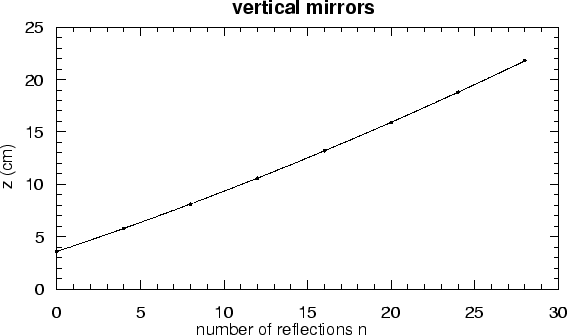
Using this fit we find a value for 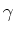 of
of 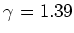 mrad.
We can evaluate the angle of incidence
mrad.
We can evaluate the angle of incidence 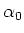 from Eq.
2.3 by using the linear term
from Eq.
2.3 by using the linear term 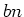 :
:
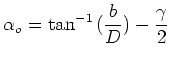 |
|
|
(2.5) |
Figure 2.4:
Correlation between the number of reflections 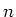 and the
position
and the
position 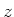 in the collimator
in the collimator
 |
We find a value for 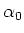 of
of 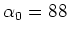 mrad. With use of this
angle
mrad. With use of this
angle 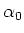 we can calculate the distance
we can calculate the distance 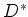 the light has to
travel from one mirror to the opposite mirror.
the light has to
travel from one mirror to the opposite mirror.
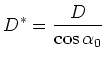 |
|
|
(2.6) |
With the value we found for the angle 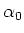 we find a value for
we find a value for 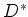 of 6.0233 cm for the pair of mirrors that cools the horizontal transverse
velocity. The values for the pair of mirrors that cools the vertical
transverse velocity are
of 6.0233 cm for the pair of mirrors that cools the horizontal transverse
velocity. The values for the pair of mirrors that cools the vertical
transverse velocity are 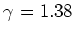 mrad,
mrad,
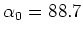 mrad and
mrad and
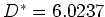 cm.
cm.
To measure the angle 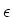 between the two mirrors, we also
measure the vertical displacement
between the two mirrors, we also
measure the vertical displacement 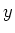 of the maximum of the laser light
for various values of
of the maximum of the laser light
for various values of 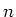 . The height of the diode can be adjusted by a
micrometer. The way to calculate the angle
. The height of the diode can be adjusted by a
micrometer. The way to calculate the angle 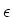 is similar to the
method of calculating
is similar to the
method of calculating 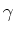 . Equation 2.3 can be
adjusted to:
. Equation 2.3 can be
adjusted to:
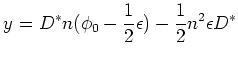 |
|
|
(2.7) |
with
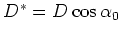 the distance the light has to travel from
one mirror to the other, and
the distance the light has to travel from
one mirror to the other, and 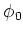 the angle of incidence as shown in
fig. 2.3. By searching the maximum intensity of the
laser light in the
the angle of incidence as shown in
fig. 2.3. By searching the maximum intensity of the
laser light in the 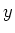 -direction at the maximum intensity in
the
-direction at the maximum intensity in
the 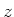 -direction for different values of
-direction for different values of 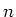 , we can fit these data
points to equation 2.7. The angle
, we can fit these data
points to equation 2.7. The angle 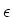 can be
calculated from:
can be
calculated from:
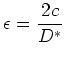 |
|
|
(2.8) |
The values found for the two pairs of mirrors are
 rad and
rad and
 rad.
rad.
Figure 2.5:
Correlation between the number of reflections n and the
position y in the collimator
 |
The angle 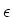 causes the light to drift away from the center of
the collimator. It is important to know what the maximum value of this
drift can be, since the light and the atomic beam should overlap as much
as possible. If the laser light is shone in with an angle
causes the light to drift away from the center of
the collimator. It is important to know what the maximum value of this
drift can be, since the light and the atomic beam should overlap as much
as possible. If the laser light is shone in with an angle
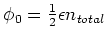 , the angle
, the angle 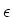 will cause the angle
will cause the angle
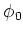 to decrease, so that it will be zero after half the total number of
reflections, and will leave the collimator with an angle -
to decrease, so that it will be zero after half the total number of
reflections, and will leave the collimator with an angle -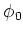 at the
same height as it is shone in, following a parabolic path through the
collimator. The maximum difference in height is the value at
at the
same height as it is shone in, following a parabolic path through the
collimator. The maximum difference in height is the value at
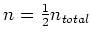 minus the value at
minus the value at 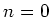 . If we use equation
2.7 to calculate the maximum difference in height,
assuming the total number of reflections
. If we use equation
2.7 to calculate the maximum difference in height,
assuming the total number of reflections 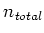 to be 40 (which is
more than the actual number of reflections), the shift is 0.45 mm. This is
small enough compared to the height of the laser light, which is 1 cm.
to be 40 (which is
more than the actual number of reflections), the shift is 0.45 mm. This is
small enough compared to the height of the laser light, which is 1 cm.




Next: Aligning the collimator
Up: The collimator
Previous: The collimator
Contents
Vincent van der Bilt
2002-12-27

![]() and
and ![]() are so small, we need a special way to
measure them. In Eq. 1.11,
are so small, we need a special way to
measure them. In Eq. 1.11, ![]() is given as a function
of the number of reflections
is given as a function
of the number of reflections ![]() . This can be rewritten to:
. This can be rewritten to:
![]() of
of ![]() mrad. With use of this
angle
mrad. With use of this
angle ![]() we can calculate the distance
we can calculate the distance ![]() the light has to
travel from one mirror to the opposite mirror.
the light has to
travel from one mirror to the opposite mirror.
![]() between the two mirrors, we also
measure the vertical displacement
between the two mirrors, we also
measure the vertical displacement ![]() of the maximum of the laser light
for various values of
of the maximum of the laser light
for various values of ![]() . The height of the diode can be adjusted by a
micrometer. The way to calculate the angle
. The height of the diode can be adjusted by a
micrometer. The way to calculate the angle ![]() is similar to the
method of calculating
is similar to the
method of calculating ![]() . Equation 2.3 can be
adjusted to:
. Equation 2.3 can be
adjusted to:
![]() causes the light to drift away from the center of
the collimator. It is important to know what the maximum value of this
drift can be, since the light and the atomic beam should overlap as much
as possible. If the laser light is shone in with an angle
causes the light to drift away from the center of
the collimator. It is important to know what the maximum value of this
drift can be, since the light and the atomic beam should overlap as much
as possible. If the laser light is shone in with an angle
![]() , the angle
, the angle ![]() will cause the angle
will cause the angle
![]() to decrease, so that it will be zero after half the total number of
reflections, and will leave the collimator with an angle -
to decrease, so that it will be zero after half the total number of
reflections, and will leave the collimator with an angle -![]() at the
same height as it is shone in, following a parabolic path through the
collimator. The maximum difference in height is the value at
at the
same height as it is shone in, following a parabolic path through the
collimator. The maximum difference in height is the value at
![]() minus the value at
minus the value at ![]() . If we use equation
2.7 to calculate the maximum difference in height,
assuming the total number of reflections
. If we use equation
2.7 to calculate the maximum difference in height,
assuming the total number of reflections ![]() to be 40 (which is
more than the actual number of reflections), the shift is 0.45 mm. This is
small enough compared to the height of the laser light, which is 1 cm.
to be 40 (which is
more than the actual number of reflections), the shift is 0.45 mm. This is
small enough compared to the height of the laser light, which is 1 cm.