Saturation spectroscopy

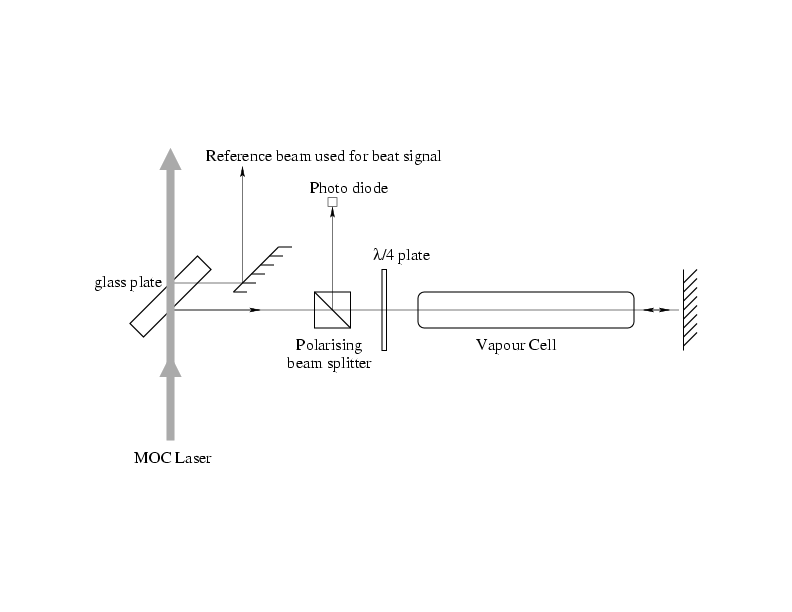
To reduce the variation in frequency of the laser light for the Magneto-Optical Compressor we used the method of saturation spectroscopy to stabilize the laser. The setup of this technique is shown in fig 2.8.

Figure 2.8: Setup of the laser stabilisation of the MOC laser.

A small part of the laser beam is split off by a glass plate, and goes through a polarizing beam splitter. The laser light that passed the polarizing beam splitter is linearly polarized, and becomes circularly polarized by the $\lambda$/4-plate.

The vapor cell is filled with He atoms at room temperature, under a pressure of 0.08 mbar, excited to the metastable state by an rf-field. The light will pass the vapor cell, is then retro-reflected at the mirror, and will pass the vapor cell and the $\lambda$/4-plate again. The polarization of the laser beam has turned 90 degrees after passing the polarizing beam splitter for the first time, and it will now be reflected on the photo diode, which measures the intensity of the laser beam. If the laser light is slightly under resonance, the atoms which have a velocity $v$ that satisfies $\omega - \omega_0 = \vec v \cdot \vec k$ will be in resonance with the laser. Since the laser shines through the vapor cell in two directions opposite to each other, there will be two classes of velocities that absorb the photons. The intensity of the laser beam will decrease.

If the laser is exactly on resonance, that is $\omega -\omega_0 = 0$, both the laser beams are in resonance with the same velocity class ( $\vec v \cdot \vec k = 0$). Since the first laser beam has already excited He* atoms to the $\vert e \rangle$ state, the second laser beam will be absorbed much less. This results in a small peak of increased intensity in the transmission signal when the laser is exactly on resonance. This peak is called the Lamb dip.

Figure 2.9: Lamb dip in the D1 and the D2 transition.

In fig. 2.9 the Lamb dip of both the D2 and the D1 transition are shown. This was done by applying a sawtooth shaped current on the fast entrance of the power supply of the laser. The intensity of the laser beam is measured with the diode, and the figure shows an average over one hundred periods.

We now add a sine shaped current with an amplitude so small that it alters the frequency of the laser only a few MHz (the current used for fig 2.9 was big enough to show both the D2 and the D1 line, which are separated by 2.299 GHz), and with a frequency of 2 KHz. If the laser is on resonance, the sine shaped current will make the laser scan over the top of the Lamb dip [7]. By integrating the signal received from the diode, multiplied by a square wave voltage with exactly the same frequency as the sine, it can be seen if the laser is exactly on top of the Lamb dip, or on one of the flanks. If the laser is exactly on resonance, the first part of the integral gives a positive value due to the square wave, and the second part gives the same, but negative value. The total sum will be zero, and no correction has to be made to the laser frequency.

If the laser frequency is slightly under resonance, the Lamb dip peak will fall in the first part of the integral, and the total sum will be positive. A frequency slightly above resonance will result in a negative sum. We use this positive or negative value to correct the frequency of the laser. This method of stabilizing the frequency is very effective, only when the laser frequency changes so fast that the Lamb dip can not be seen within the amplitude of the scan signal, the laser can get unlocked, but under normal circumstances the laser could be locked on resonance for hours.

The lasers that we use need to have a frequency that is slightly detuned to the red from resonance. The method of locking the laser frequency as described above can still be used, but to compensate for the change in frequency, we must add a magnetic field over the vapor cell. Since we use $\sigma^+$ light, the used transition will be the transition from the He($2^3$S$_1$, m=1) to the He($2^3$P$_2$, m=2) state. The change in energy separation between these two states caused by the applied magnetic field can be calculated with use of equation 1.6, and is found to be:

$$\Delta E_{B_z} = \mu_B B_z$$ (2.9)

This gives a change in frequency of 1.4 MHz per Gauss applied over the vapor cell. The MOC laser needs a detuning to the red of a few $\Gamma$, with $\Gamma =1.6$ MHz. The magnetic field is supplied by a coil of copper wire, outside the aluminum box which has been placed around the vapor cell to shield the above mentioned rf-field from disturbing other electronic instruments. The coil should be long enough and neatly winded, to give a homogeneous magnetic field over the whole vapor cell.