



Next: Theory of the collimator
Up: Theory
Previous: Theory
Contents
Theory of laser cooling
Consider a two level atom with ground state 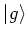 and excited
state
and excited
state 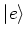 . There are three processes taking place when this atom
is put in a resonant electro-magnetic field (see fig.
1.1).
The absorption
of one photon excites the atom from the
. There are three processes taking place when this atom
is put in a resonant electro-magnetic field (see fig.
1.1).
The absorption
of one photon excites the atom from the 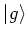 to the
to the 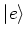 state, and a momentum of
state, and a momentum of 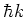 is transferred to the atom in the
direction of the photon, with
is transferred to the atom in the
direction of the photon, with
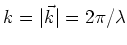 , and
, and
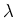 the wavelength of the photon.
the wavelength of the photon.
Figure 1.1:
Absorption and emission of a two level atom
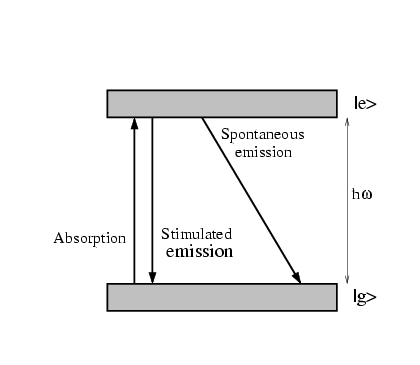 |
If the atom is in the 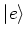 state, it can emit a photon by
stimulated emission, which would cause a momentum transfer of
state, it can emit a photon by
stimulated emission, which would cause a momentum transfer of 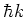 in
the direction opposite to the photon. The third process is
called spontaneous emission. The atom falls back to its ground state,
emitting a photon in a random direction.
An absorption/stimulated emission cycle has no net momentum transfer to
the atom, since the momentum transfers are equal and opposite to each
other. When an atom goes through
in
the direction opposite to the photon. The third process is
called spontaneous emission. The atom falls back to its ground state,
emitting a photon in a random direction.
An absorption/stimulated emission cycle has no net momentum transfer to
the atom, since the momentum transfers are equal and opposite to each
other. When an atom goes through 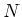 absorption/spontaneous
emission-cycles, it
will experience a net momentum transfer of
absorption/spontaneous
emission-cycles, it
will experience a net momentum transfer of 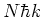 due to the
absorption, and no net momentum transfer due to the spontaneous
emission, since these photons are emitted in a random direction.
With this technique it is possible to alter the velocity of neutral atoms
by using laser light with a frequency of
due to the
absorption, and no net momentum transfer due to the spontaneous
emission, since these photons are emitted in a random direction.
With this technique it is possible to alter the velocity of neutral atoms
by using laser light with a frequency of
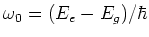 ,
with
,
with 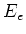 the energy level of the excited state, and
the energy level of the excited state, and 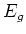 the energy
level of the ground state.
the energy
level of the ground state.
The maximum force exerted on an atom by a
resonant electro-magnetic field with frequency 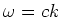 is given by:
is given by:
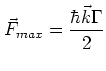 |
|
|
(1.1) |
in which 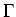 =
= 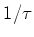 is the spontaneous decay rate.
If the light intensity is low, the absorption profile of the transition
is given by the Lorentz profile
is the spontaneous decay rate.
If the light intensity is low, the absorption profile of the transition
is given by the Lorentz profile 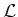 :
:
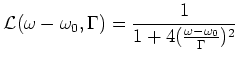 |
|
|
(1.2) |
with 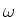 the frequency in the rest frame of the atom, and
the frequency in the rest frame of the atom, and 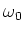 the transition frequency.
The chance that a photon with frequency
the transition frequency.
The chance that a photon with frequency 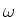 will be absorbed by the
atom, is proportional to the value of the Lorentz profile.
The width of this transition is defined as the full width half maximum
value:
will be absorbed by the
atom, is proportional to the value of the Lorentz profile.
The width of this transition is defined as the full width half maximum
value:
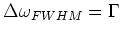 |
|
|
(1.3) |
For larger values of the intensity 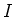 of the laser light, the
transition width is broadened according to:
of the laser light, the
transition width is broadened according to:
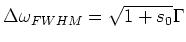 |
|
|
(1.4) |
Here 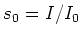 is the saturation parameter, with
is the saturation parameter, with 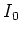 the saturation
intensity, and
the saturation
intensity, and 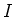 the intensity of the laser light.
For large intensities of the laser light, this can be approximated by
the intensity of the laser light.
For large intensities of the laser light, this can be approximated by
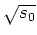 .
.
The force on the atom is dependent on the intensity and the frequency
of the laser light used [3]:
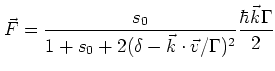 |
|
|
(1.5) |
with
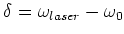 is the detuning of the
laser.
The term
is the detuning of the
laser.
The term
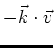 is the Doppler shift.
is the Doppler shift.
When the atom is placed in a magnetic field, the energy levels of the atom
will shift by an amount of
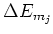 [4]:
[4]:
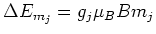 |
|
|
(1.6) |
due to the Zeeman effect. Here 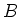 is the applied magnetic field,
is the applied magnetic field, 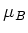 the Bohr magneton, and
the Bohr magneton, and 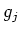 the Landé factor, depending on the
quantum numbers
the Landé factor, depending on the
quantum numbers 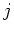 ,
, 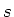 and
and 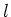 :
:
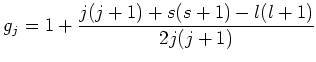 |
|
|
(1.7) |
This change in the energy levels causes a shift in the frequency
 , so that the total detuning of the laser becomes:
, so that the total detuning of the laser becomes:
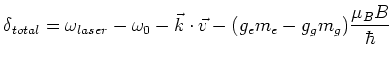 |
|
|
(1.8) |
Figure 1.2:
Two level scheme of triplet He
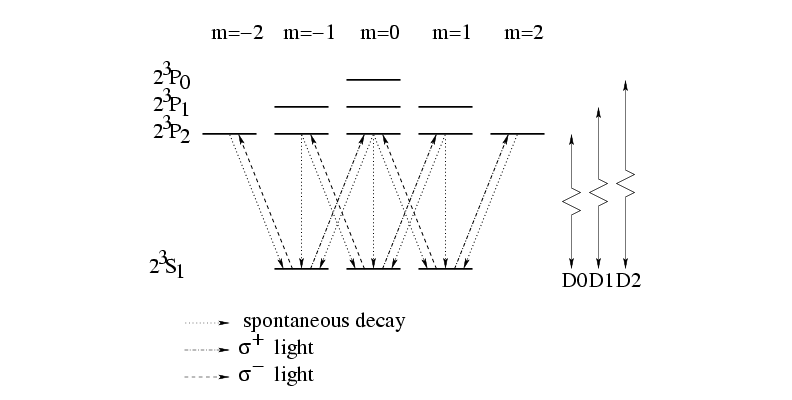 |
The two state atom used in our experiments is He*, or metastable
helium, and the two states are He(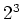 S
S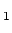 ) (ground state) and
He(
) (ground state) and
He(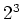 P
P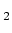 ) (excited state)(see fig. 1.2). This
transition is called the D2 transition. The transition from
He(
) (excited state)(see fig. 1.2). This
transition is called the D2 transition. The transition from
He(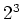 S
S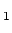 ) to He(
) to He(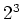 P
P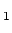 ) is called the D1 transition, and has an
energy difference between the two states very close to the energy
difference of the D2 transition.
) is called the D1 transition, and has an
energy difference between the two states very close to the energy
difference of the D2 transition.
The reason that He(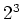 S
S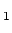 ) can be used
as a ground state is that it has a lifetime of 8000 s, which is much
longer than the flight time of the atoms in our setup (5-10 ms).
By choosing the polarization of the laser light, the atoms can be
optically pumped to the
) can be used
as a ground state is that it has a lifetime of 8000 s, which is much
longer than the flight time of the atoms in our setup (5-10 ms).
By choosing the polarization of the laser light, the atoms can be
optically pumped to the 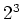 S
S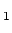 (m
(m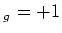 ) (
) (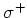 light) or to the
light) or to the
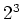 S
S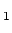 (m
(m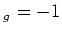 )
(
)
(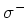 light), because the spin selection rules demand that
light), because the spin selection rules demand that 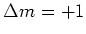 and
and 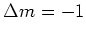 for
for 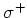 resp.
resp. 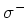 light.
light.
The wavelength of the laser light used for the D2 transition is
1083.034 nm, which is in the infrared regime. The saturation intensity for
this transition is 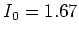 W/m
W/m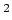 , and
, and 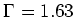 MHz.
With the diode laser used for our experiments, we could detune a few
gigahertz, so that we could also see the D1 transition, which lies 2.299
GHz above the D2 transition.
MHz.
With the diode laser used for our experiments, we could detune a few
gigahertz, so that we could also see the D1 transition, which lies 2.299
GHz above the D2 transition.




Next: Theory of the collimator
Up: Theory
Previous: Theory
Contents
Vincent van der Bilt
2002-12-27
![]() and excited
state
and excited
state ![]() . There are three processes taking place when this atom
is put in a resonant electro-magnetic field (see fig.
1.1).
The absorption
of one photon excites the atom from the
. There are three processes taking place when this atom
is put in a resonant electro-magnetic field (see fig.
1.1).
The absorption
of one photon excites the atom from the ![]() to the
to the ![]() state, and a momentum of
state, and a momentum of ![]() is transferred to the atom in the
direction of the photon, with
is transferred to the atom in the
direction of the photon, with
![]() , and
, and
![]() the wavelength of the photon.
the wavelength of the photon.
![]() is given by:
is given by:
![]() [4]:
[4]:
![]() S
S![]() ) (ground state) and
He(
) (ground state) and
He(![]() P
P![]() ) (excited state)(see fig. 1.2). This
transition is called the D2 transition. The transition from
He(
) (excited state)(see fig. 1.2). This
transition is called the D2 transition. The transition from
He(![]() S
S![]() ) to He(
) to He(![]() P
P![]() ) is called the D1 transition, and has an
energy difference between the two states very close to the energy
difference of the D2 transition.
) is called the D1 transition, and has an
energy difference between the two states very close to the energy
difference of the D2 transition.
![]() S
S![]() ) can be used
as a ground state is that it has a lifetime of 8000 s, which is much
longer than the flight time of the atoms in our setup (5-10 ms).
By choosing the polarization of the laser light, the atoms can be
optically pumped to the
) can be used
as a ground state is that it has a lifetime of 8000 s, which is much
longer than the flight time of the atoms in our setup (5-10 ms).
By choosing the polarization of the laser light, the atoms can be
optically pumped to the ![]() S
S![]() (m
(m![]() ) (
) (![]() light) or to the
light) or to the
![]() S
S![]() (m
(m![]() )
(
)
(![]() light), because the spin selection rules demand that
light), because the spin selection rules demand that ![]() and
and ![]() for
for ![]() resp.
resp. ![]() light.
light.
![]() W/m
W/m![]() , and
, and ![]() MHz.
With the diode laser used for our experiments, we could detune a few
gigahertz, so that we could also see the D1 transition, which lies 2.299
GHz above the D2 transition.
MHz.
With the diode laser used for our experiments, we could detune a few
gigahertz, so that we could also see the D1 transition, which lies 2.299
GHz above the D2 transition.