TOF measurements at different detunings

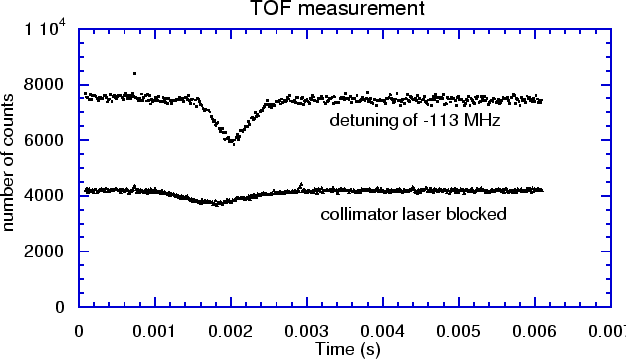
We want to see what the effect of the collimator is on the velocity distribution of the metastable He atoms. In fig 3.5 the TOF measurement of the unaltered He* beam is shown together with the measurement of the collimated He* beam. Both of the measurements lasted 5 minutes. It can be seen that the total signal of the collimated beam is about a factor 2 higher than the uncollimated beam. The dip in the collimated beam is much larger, since a much higher percentage of the detected particles is metastable Helium.

Figure 3.5: The channeltron signal of the TOF measurement, with and without collimator lasers.

Another interesting thing that can be seen from fig 3.5 is that the width of the dip is much smaller for the collimated beam. This can be explained by the fact that the collimator works as a velocity selective device [2]. The angle $\alpha_0$ with which the laser shines in the collimator, should compensate the detuning of the laser by creating a Doppler shift with the parallel He* atoms that leave the collimator. This Doppler shift is given by $-\vec k \cdot \vec v$. This means that the collimator affects a different part of the velocity distribution for different detunings of the laser. From the measurement in sec 3.3 we found that the best detuning for the collimator was around the -110 to -115 MHz. At this detuning the collimator is the most effective for velocities around the 1000 m/s, which is the peak velocity in the distribution.

We have performed a series of TOF measurements at different detunings of the collimator laser to see what the effect of the collimator is on the velocity distribution of the He* beam. These measurements were done over the frequency range of -150 MHz to -80 MHz. At all detunings we calculated the mean speed of the atoms as well as the velocity spread.

Figure 3.6: The mean speed of the collimated He* atoms at different detunings for the collimator laser.

In fig 3.6 we can see the dependency of the mean speed of the He* atoms to the frequency of the collimator laser. If the collimator is detuned further to the red, the collimator is effective for atoms with a higher velocity. This is what we expected, since the detuning of the laser and the velocity of the atoms are related by:

$$\omega_0 - \omega_{laser} = kv \sin{\alpha_0}$$ (3.2)

and the angle $\alpha_0$ has not changed during the measurements. We calculated the mean speed by subtracting the TOF measurement without the collimator from the TOF measurement with the collimator. In this way we calculate the mean speed of the increased signal, which is the mean speed of the atoms that were affected by the collimator. The problem with this method is that especially for the measurements with only one dimension of the collimator working, the increased signal is too small at detunings far away from the optimal detuning to make a good fit to these data. The measurements at a detuning of -90 MHz could not be used, since it was not possible to fit a distribution to the data.

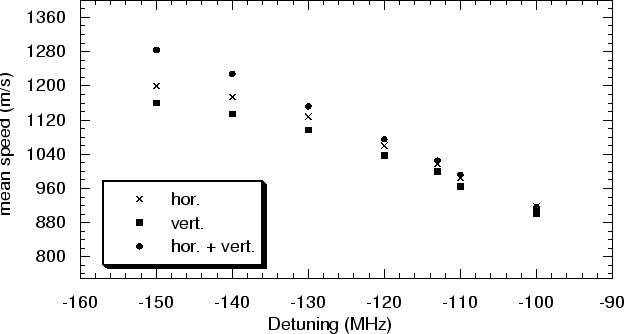The measurement in which the collimator was working in both dimensions shows a linear dependency between the detuning and the mean speed of the collimated He* atoms. With only one dimension of the collimator working, the increase of the mean speed of the collimated atoms is smaller at higher detunings. This could be explained by the fact that for higher detunings a higher velocity is in resonance with the laser light. These faster atoms have a shorter interaction time with the laser light in the collimator. This means that the faster atoms are less effectively collimated, so that the gain of faster atoms is relatively smaller than for the slower atoms. This results in a lower mean speed $\bar v$ than expected.

If we make use of the formula 3.2 and rewrite it to:

$$\alpha_0 = \sin^{-1}(\frac{\omega_0 - \omega_{laser}}{k v})$$ (3.3)

we can calculate the value of the angles $\alpha_0$, since $k = 5.806\cdot 10^6$ m$^{-1}$, and $v/(\omega_0 - \omega_{laser})$ is the slope of the linear fit through the data of fig 3.6. If we calculate the angles $\alpha_0$ with use of the slope of the linear fit trough the data points we find $\alpha_{0_{hor}} = 0.155$ rad and $\alpha_{0_{vert}} = 0.165$ rad. A combined angle can be calculated from the third set of data points, and results in a value $\alpha_{0_{h+v}} = 0.137$ rad. All three values are bigger than the minimum value $\alpha_0 = 0.133$ rad, calculated in sec. 1.2.1.

Figure 3.7: The velocity spread of the collimated He* atoms at different detunings for the collimator laser.

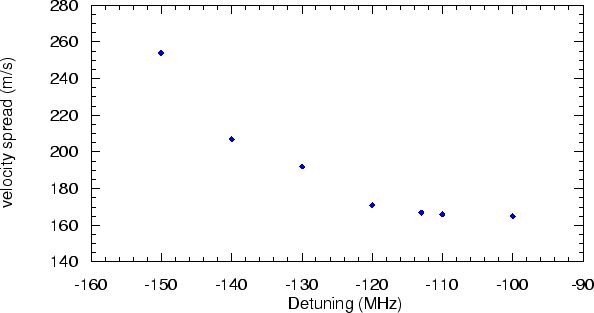For the situation with two dimensions of the collimator working, we also looked at the velocity spread of the collimated atoms. The results can be seen in fig 3.7. The velocity spread is for all detunings smaller than the velocity spread of the uncollimated atoms. For detunings further to the red, the velocity spread is higher, and for detunings closer to resonance the velocity spread seems to converge to a value of about 160 m/s. An explanation of this effect could be that the atoms affected by the lower detunings have a lower speed and therefor a longer interaction time in the collimator. At higher detunings the atoms are too fast to stay in resonance with the collimator and there is not a specific class of velocities that is completely collimated. For the detuning of -113 MHz, which was the optimal detuning for the collimator, the spread of the atoms is about 170 m/s, so the atoms can stay in resonance through the collimator for this detuning. The converging limit of 160 m/s is caused by the intensity of the laser light, with a higher $s_0$ the transition width of the collimator laser is larger, and a larger class of velocities can be affected. The width of the transition is given by Eq. 1.4, with $s_0 = 139$ (average of the four laser beams entering the collimator), and $\Gamma = 10.2 \cdot 10^6$rad/s. This width of transition will give a range of velocities $v$ that is affected by the laser light:

$$\sqrt{1+s_0} \Gamma = k \Delta v \sin{\alpha_0}$$ (3.4)

Using $\alpha_{0_{h+v}}$, we find a velocity spread of $\Delta v = 152$ m/s, which is very close to the converging limit of 160 m/s that we found in the experiment.